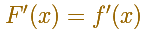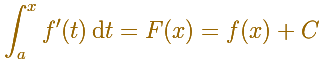4.1.4 Sistemas de ecuaciones equivalentes.
Los sistemas de ecuaciones equivalentes son los que tienen el mismo conjunto de soluciones, aunque tengan distinto número de ecuaciones.
Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes. Si:
Todos los coeficientes son ceros.
Dos ecuaciones son iguales.
Una ecuación es proporcional a otra.
Una ecuación es combinación lineal de otras.
Criterios de equivalencia de sistemas de ecuaciones
1 Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.
2 Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.
3 Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.
4 Si en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.
5 Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.
MODELO APA:
http://www.vitutor.com/algebra/sistemas%20I/equi.html
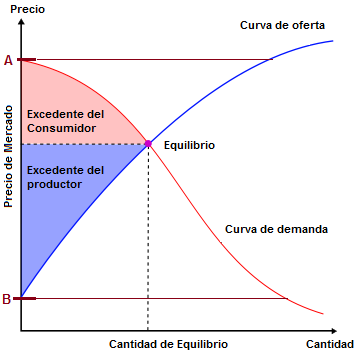
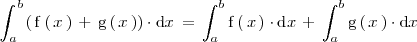
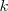 por una función es igual al producto de
por una función es igual al producto de 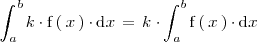
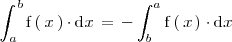
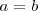 en la igualdad anterior se tiene que
en la igualdad anterior se tiene que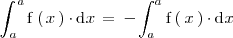
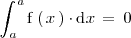
 .
.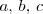 se tiene que:
se tiene que: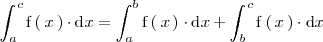
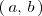 la función
la función  es mayor o igual que la función
es mayor o igual que la función 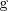 entonces
entonces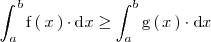
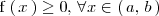 , entonces
, entonces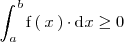
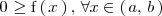 , entonces
, entonces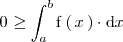
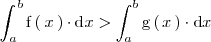
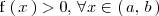 , entonces
, entonces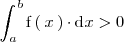
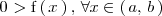 , entonces
, entonces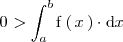
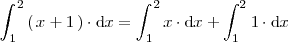
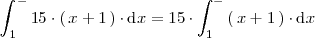
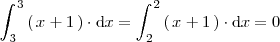
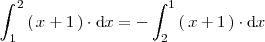
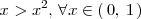 , se cumple que
, se cumple que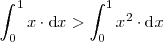
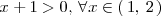 , se cumple que
, se cumple que